题目:
有64匹马,8个跑道,要找出跑得最快的4匹马,要比赛最少多少轮?
分析:
即每轮可以确定8匹马的相对速度,肯定需要假设每次马的速度恒定。首先64匹马都需要先上场跑一趟,64匹都跑了一圈之后我们能得到哪些信息?
- 每组中的8匹马的相对速度可以确定
然后就直接取每组的前4匹继续跑吗,当然不行。这个已有信息利用得也太少了。每组内相对速度确定,说明每组内已经是有序的,一共有8组,最终只取4匹。显然最多会从4组中抽选出结果,另外4组一定是无用的。但又不能确定哪4组直接淘汰,于是可以通过每组第一来建立它们的联系。
求解过程:
通过上面分析,可以将8组中各自的第一名放一起比较。得到它们的排名,便可以直接淘汰掉最后4组。并且剩下的4组也可以直接去掉每组内的最后4名。现在就变成了$4\times 4 = 16$匹马之间的筛选。值得注意的是刚刚8个第一名一起跑的结果确定了它们之间的相对速度,也就是这4组的第一之间的速度是确定的。
现假设这4组分别为$A,B,C,D$,其中$A=\{ A1,A2,A3,A4 \}$,且$A1>B1>C1>D1$ 。其情况可表示如下

如果现在将其拆分为两组继续比较,还需比较3轮,但是在这里面是有较多已有序结构的。我们的目的是确定前4名,虽不能通过一些方法直接确定哪些“是”,但可以通过已有顺序来确定哪些“不是”。
这个也很简单,连线就行了
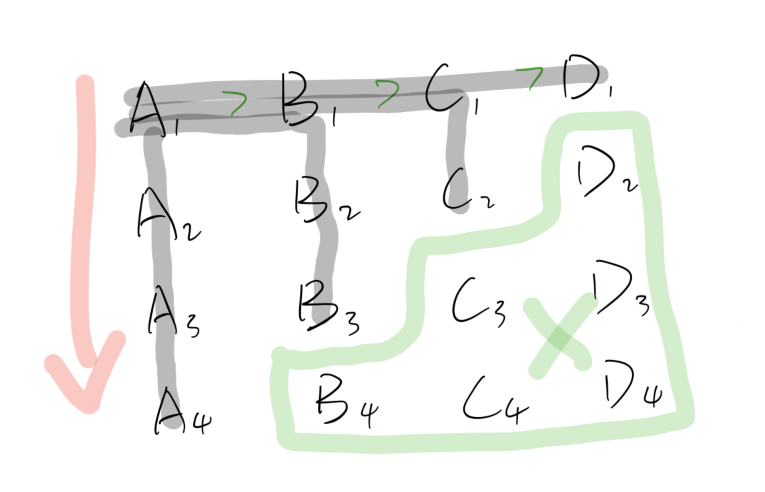
按照已知的顺序,绿圈内的马匹是一定在第4名开外的。因此剩下的任务只是从这10匹马中选出前4名。而最快的一定是$A1$。于是变成9选3。
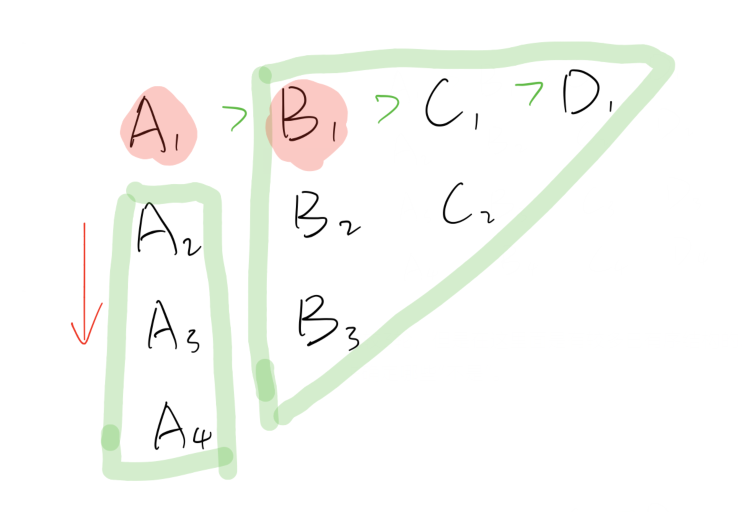
在剩下的9匹马中,$A1,A2,A3$的顺序确定,而在$B1$圈中,$B1$的地位和原来圈中$A1$的地位是相同的。9选3,两轮肯定可以完成了,但是否可以再利用一下这些相对顺序偷偷懒呢,可以试一试,两个圈子中最大的分别是$A2,B1$,如果在除了它们剩下的8匹马中选2个,其中前两名有它们的“小弟”在,那么它们一定在前3名。$A2,B1$选哪个呢,当然是$B1$,因为它“小弟”多。
8选2,现讨论前两名的情况:
- 当前两名中含有$C1$或$B2$时,$B1$一定是前4名。其中,若$C1,B2$在前两名中的第一位置,那么$B1$的最终位置是确定的,但若第一是$A2$,则$B1$位置不确定,但一定是前4名。
- 若前两名是$A2,A3$,则需要看第3是谁,如果是$C1,B2$,则$B1$也能保证是前4,但位置不确定。
- 若$B1$的小弟一点也不给力,前三是$A2,A3,A4$,则不能确定$B1$是否能进前4,需要$B1$亲自与它们跑一次。
由此,可以得到结论:
先跑8轮确定组内排名,再让各组第一跑一轮,确定组间老大地位。至此可淘汰至$4\times 4$。再根据已有的组间老大顺序和组内顺序,可以淘汰不可能选上的6匹,剩下10匹。其中最快的已确定,9选3。除去$B1$,让剩下的8匹跑,若$B1$的“小弟”给力,就能直接确定前4。如若不然,则需再加一轮。因此总的轮数是10或者11。






