实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 true
trie.search(“app”); // 返回 false
trie.startsWith(“app”); // 返回 true
trie.insert(“app”);
trie.search(“app”); // 返回 true
说明:
你可以假设所有的输入都是由小写字母 a-z 构成的。
保证所有输入均为非空字符串。
前缀树是一种比较简单的数据结构,又名字典树。就像这个名字一样,它将输入的词汇按从前到后的字符进行索引,就像查单词时挨个输入的字符的情形。每个位置有26个可能(假设都为小写字母),因此它是一个26叉树。比如对abc,abd,ac,bc建立一个字典树
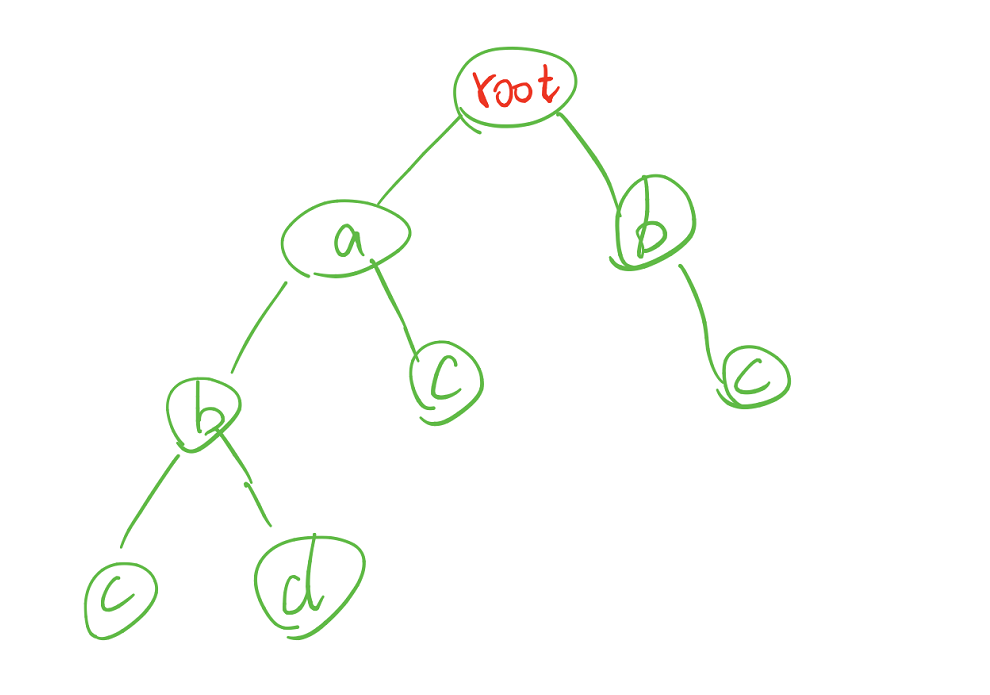
可见,当数据的前缀有较多重复的时候,字典树可以节约较多内存。但是若杂乱无章的话可能反而增加内存消耗,因为字典树需要开辟空间来保存节点信息。图中可以看出字典树的两个特点
- 根节点不含字符信息
- 从根节点到某个节点途径的节点连接起来就是该节点的字符串组成
再来看看一个基本的字典树节点需要包含哪些信息。首先需要26个指针来指向下一个节点,可以使用指针数组来方便管理,并且字典树中的数据是有确定范围的,就是26个字母,因此数组的下标就能表示下一节点的字母是什么。还需要一个标志位来表示某节点是否是一个字符串的结尾,这样才能在查询时确认是否是原始输入字符串或是该字符串的子串。
1 | //C++ 70ms 44MB |
数组模拟Trie树
数组模拟的思想是使用二维数组,其中第一维表示树节点,第二维表示每个节点的子节点(字符),一个关键是用下标来建立它们之间的关系。
每个节点内保存的都是下一个节点的下标,如果节点内容为0,则表示该节点为空节点。建立的过程中,下标是单增的,保证每个节点的唯一性。
1 | const int N = 1e5+10; |